Un joven de 16 años ha logrado resolver un enigma matemático planteado por Isaac Newton hace más de 350 años. Shouryya Ray, el joven prodigio que ha sorprendido a la comunidad científica, es un alumno de origen indio que estudia en una escuela secundaria de Dresden, en Alemania.
Ray emigró a Dresden desde Calcutta hace cuatro años sin hablar ni una palabra de alemán, un idioma que ahora domina. Sus profesores se dieron cuenta en poco tiempo de que poseía una inteligencia extrordinaria, y le permitieron saltarse dos cursos para que se encontrara en el nivel adecuado para sus capacidades.
Su habilidad para las matemáticas también se debe sin duda a que desde que era muy pequeño, su padre, un ingeniero, le desafiaba con problemas aritméticos. De hecho, antes de cumplir 10 años ya era capaz de resolver ecuaciones complejas.
Ha logrado resolver dos teorías de dinámicas de partículas que hasta ahora los físicos sólo podían calcular de manera aproximada con potentes ordenadores.
Gracias a sus ecuaciones, ahora se podrá calcular con exactitud la trayectoria de un proyectil afectado por la gravedad y por la resistencia del aire (el problema propuesto por Newton hace más de tres siglos), y también predecir cómo golperará y rebotará en una pared.
El joven descubrió los problemas planteados por Newton durante una visita escolar a la Universidad de Dresden, en la que los profesores le explicaron que eran enigmas "irresolubles". Ahí le ofrecieron datos experimentales con los que analizar la trayectoria del lanzamiento de una pelota. Los métodos para resolverlo eran aproximaciones y Ray decidió -«por curiosidad e ingenuidad de estudiante», explicó a 'The Sunday Times'- buscar la solución definitiva.
"Me pregunté a mí mismo: ¿por qué no intentarlo?", recuerda el joven. "No me podía creer que no existiera una solución".
Ray afirma que disfruta mucho de la "belleza intrínseca" de las matemáticas, pero asegura con humildad que no es "ningún genio", y confiesa que le gustaría también destacar en otras actividades, además de las matemáticas. "Me encantaría jugar mejor al fútbol", ha reconocido al diario británico 'The Daily Mail'.
29 mayo 2012
El problema de Newton y la solución que ha obtenido Shouryya Ray (16 años)
Me da vergüenza tener que escribir esta entrada. Una noticia del periódico sensacionalista Daily Mail ha copado muchos medios (El Mundo,20 minutos, Sur Málaga, La Vanguardia, etc.). Hasta mi buen amigo Gaussianos, el divulgador matemático español por excelencia, ha caído en la trampa de la noticia “Shouryya Ray, genio de 16 años que ha resuelto un problema propuesto por Newton hace más de 300 años,”gaussianos, 27 mayo, 2012. Basta ver la foto de la solución obtenida para saber que el chaval ha resuelto un problema de primer curso de física (que viene en todos los libros de texto): el movimiento de un proyectil sujeto a la aceleración de la gravedad y a una fuerza de rozamiento; para los que no sepan qué son los símbolos de esta ecuación les aclaro que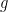 
es la aceleración de la gravedad, 
son las componentes de la velocidad del proyectil, 
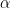es la constante que multiplica a la fuerza de rozamiento, y 
es la función arcoseno hiperbólico. ¿Obtener esta solución permite comparar a este muchacho con Ramanujan? ¡De vergüenza! ¡Cómo es posible que haya tanta ignorancia matemática!
es la aceleración de la gravedad, son las componentes de la velocidad del proyectil, es la constante que multiplica a la fuerza de rozamiento, y es la función arcoseno hiperbólico. ¿Obtener esta solución permite comparar a este muchacho con Ramanujan? ¡De vergüenza! ¡Cómo es posible que haya tanta ignorancia matemática!
A partir de una versión de mayor resolución de esta foto del póster del muchacho, se puede reconstruir fácilmente su logro. Las ecuaciones que ha resuelto el muchacho son las siguientes
Toda persona que haya estudiado un primer curso de física sabrá obtener estas ecuaciones a partir de las leyes de Newton. ¿Te atreves? Toda persona que haya estudiado la resolución de ecuaciones diferenciales de primer orden (primer curso de matemáticas) debería estar en posición para resolver estas ecuaciones sin ninguna dificultad. ¿Te atreves? ¡Ah, qué no las ves bien! Te las copio en LaTeX.
Bueno, si no eres matemático, o físico, o ingeniero, o tienes oxidados tus conocimientos, te recuerdo el cambio de variable conocido para resolver este sistema de ecuaciones desde principios del s. XVIII, que es el mismo utilizado por el chaval.
El cambio de variable estándar 
, conduce trivialmente a la ecuación de primer orden
, conduce trivialmente a la ecuación de primer orden
La solución de esta ecuación es trivial de obtener; si no sabes, ¡qué torpe!, puedes usar Mathematica para obtener la solución que aparece en la primera foto de esta entrada (que en la foto del póster aparece truncada).
¿Por qué se dice que Newton no obtuvo la solución de este sistema? Porque Newton en los Principia presentó varias soluciones en forma de series y en concreto para esta ecuación utilizó una serie que aparece en el propio póster del chaval como
Obviamente, esta solución poco satisfactoria fue escrita en forma cerrada unos pocos años después de la publicación de los Principia. Pero un chaval de 16 años no tiene por qué saberlo.
¿No dicen que el chaval ha obtenido dos soluciones? ¿Dónde está la otra? En la parte final del póster… huelgan más comentarios.
Si eres profesor de física o matemáticas de primer curso, ¿por qué no le pones este problema a tus alumnos y compruebas si son capaces de emular el gran logro matemático del nuevo “genio” Ray? Es broma…
No hay comentarios:
Publicar un comentario